This is on-going work and will be updated regularly.
The Stirling Engine
Abstract —This
review attempts to provide an investigation into the thermodynamic analysis of a
Stirling engine.
The Stirling Engine
Nomenclature
CV specific heat at constant volume (J/kg K)
e Stirling engine thermal efficiency (%)
n mole number
p absolute pressure (N/m2)
Q heat
Qh heat furnished by the heater (J)
Qk heat furnished by the cooler (J)
R gas constant (J/kg K)
U internal energy (J)
T temperature (K)
Th heater temperature (K)
Tk cooler temperature (K)
V volume (m3)
Vh heater volume (m3)
Vk cooler volume (m3)
Vm minimum volume considering Vh and Vk only (m3)
CV specific heat at constant volume (J/kg K)
e Stirling engine thermal efficiency (%)
n mole number
p absolute pressure (N/m2)
Q heat
Qh heat furnished by the heater (J)
Qk heat furnished by the cooler (J)
R gas constant (J/kg K)
U internal energy (J)
T temperature (K)
Th heater temperature (K)
Tk cooler temperature (K)
V volume (m3)
Vh heater volume (m3)
Vk cooler volume (m3)
Vm minimum volume considering Vh and Vk only (m3)
VM maximum volume considering Vh and Vk only (m3)
W work (J)
Wh work for the heater piston (J)
Wk work for the cooler piston (J)
Wt engine net work (J)
W work (J)
Wh work for the heater piston (J)
Wk work for the cooler piston (J)
Wt engine net work (J)
I. INTRODUCTION
|
|
The Stirling engine was invented in 1816 by
Robert Stirling (Stirling 1816). The engines’ working principles are based on the laws of
thermodynamics and ability of volume expansion of ideal gases at different
temperatures. Although, further development of the engine was mitigated by the
quick advancement of internal-combustion and the electric motor, later years
saw lengthy amounts of investigations related to the further development of the
Stirling engine (Senft, Senft 1993, Thombare, Verma 2008). In contrast to the modern combustion engine there is no explosion
inside the cylinder during operation. Instead, the engine uses an external
heat source which results in chamber gas expanding and compressing cyclically and
repeatedly to produce motion. As a result, a wide variety of heat sources such
as solar, combustion of any fuel, nuclear and even geothermal, can be utilised and the compressible fluid gas can range from air, hydrogen, helium, nitrogen
or vapour (Abuelyamen, Ben-Mansour 2018, Hachem, Gheith et al. 2015). In certain applications the engines displays high performance and
its’ service can be desirable in situations where a long warm-up period is warranted,
quiet operation is required, multi-fuelled characteristics is required or slow
changing of engine output power is warranted (Kongtragool,
Wongwises 2003).
Figure 1 modern Stirling Engine
Geometry & Operation
Stirling engines are
commonly found in three different configurations. They have the same
thermodynamic cycle but differ in mechanical design characteristics. These
consist of the alpha, beta and gamma. The alpha type consist of twin power
pistons separate cylinders (Fig. 2.). One cylinder is exposed to a heat source
while the other is subjected to a cold temperature source.
Figure 2 alpha type configuration
Both cylinders are
connected to each other by a connecting pipe which is usually fitted with
regenerative material. The purpose of the regenerator is to improve the thermal
efficiency. The beta type vary's from the alpha by incorporating only one
cylinder. Inside this cylinder holds one sealed piston and a displacer (Fig. 3.).
Figure 3 beta type configuration
Heat is applied to the
top end whilst the bottom end is cooled. The displacers function is for
transferring gas from the hot end to the cool end during the compression and
expansion process. The power piston is fixed at ninety degrees out of phase
with the displacer piston (Abuelyamen, Ben-Mansour 2018). The gamma-type engine is similar to the beta-type. Main difference
being the cooling chamber is shifted to a small cooing chamber (Fig. 4.).
figure 4 gamma type configuration
The theoretical Stirling cycle consists of four transformations of an ideal gas between two constant temperature heat sources and separated by a heat exchanger called a regenerator (Hachem et al. 2015). It consists of two isothermal and two isochoric processes (Fig. 5.).
figure 5 Stirling cycle
Heat is applied to the hot side which subsequently results in increased gas temperature. This in turn creates a rise in pressure which pushes the work piston down. Next the displacer piston pushes cold air into the hot end. During this phase, the cooler air creates decreased pressure, causing a contraction in the gas, thereby pulling the power piston back up. Stored energy in the rotating flywheel also assists with this phase shift (Urieli, Berchowitz 1984).
Prior Knowledge
Many studies have been
carried out about modeling and analysis of the Stirling engine (Chahartaghi, Sheykhi 2018). More than twenty sets of parameters like pressure, temperature,
engine working frequency, power piston and displacer geometries, heat-exchanger
geometries have direct effect on engine output power and efficiency and they
add complication to the design procedure (Hooshang, Askari Moghadam et al. 2015). To analyze the conversion of energy from one form to another, the
availability of energy to do work, and how heat will flow, it is important to
understand the laws and applications of thermodynamics. In terms of the Stirling engine, the emphasis
is on engineering thermodynamics as it involves the process of transforming
useful work from heat (Lorentzen
1981).
By observing the first
law of thermodynamics, we examine two situations. First, consider adding heat
to a system of fixed volume. Then the internal energy increases by an amount equal
to heat added:
The second case to
consider is expansion of a gas which pushes a piston. In this case if no heat
is added to or removed from the system, the internal energy of the system
decreases by an amount equal to the work done by the system:
Considering both cases, the
internal energy can be written as:
This is the first law of
thermodynamics. From this heat can be written as:
This means that the
internal energy of the system is related to its temperature. Furthermore, heat
can be transferred into or out of the system both by a temperature gradient
and by work done by the system (Halliday, Resnick et al. 2013, Young, Freedman et al. 2010).
Theoretically, the thermal
efficiencies of the Stirling engine are close to the Carnot cycle, therefore
they have higher values of thermal efficiency than other heat engines (Batmaz, Üstün et al. 2008). The Carnot cycle (Fig. 6.), founded by French physicist Sadi
Carnot in 1824, is a glorified representation of the operation of the steam
engine. The process is such that an ideal gas is restricted in a cylinder by a
piston, and is allowed to absorb heat from a reservoir held at Th or to reject heat to a
reservoir held at Tk.
figure 6 Ideal Carnot cycle
The gas is led through a
cyclical path which, overall converts heat into useful work (Kerker 1960).
During the isothermal compression (segment 4-1 in figure 6 and 1-2 in figure
5), the cold piston moves towards the regenerator. In the following step (segment
1-2 figure in 6 and 2-3 figure in 5) both pistons move similarly so that the
volume remains constant and the working fluid is transferred through the
regenerator. This step is followed by the isothermal expansion process (segment
2-3 in figure 6 and 3-4 in figure 5), with only the hot piston moving. In the
step (segment 3-4 in figure 6 and 4-1 in figure 5) both pistons move keeping
the volume constant and transferring the working fluid through the regenerator.
This is an ideal cycle assuming the perfect heat transfer and does not take
into account heat losses during the regeneration (Puech, Tishkova 2011). For each cyclic process, heat Qh is added from the hot reservoir Th to the engine (Fig. 7.) and the engine does work W by using that heat. The heat that is not converted to work, Qk = Qh - W, leaves the engine and is dumped into the cold reservoir at Tk (Young et al, 2010, Halliday, et al, 2013).
figure 7 The heat engine
Various research and
inventions have been undertaken into improving the efficiency of Stirling
engines for both motion and power generation. One such example is the United
States patent number 3,513,659 which is for an invention for a Stirling Cycle
Amplifying Machine (Fig. 9.). This invention aims to produce a large amount of
output energy from a small amount of input energy.
figure 7 The heat engine
Calculating Efficiency
Data gathered from the Stirling engine cycle can
also be displayed in a pressure p
versus volume V diagram (Fig. 8.).
figure 8 The P V diagram
Here the product of pressure and
volume represents a quantity of work. This is the area enclosed by the four
curves of the PV diagram.
As mentioned earlier, referring to the second law of thermodynamics it is
possible to show that no heat engine can be more efficient than a reversible
heat engine working between two fixed-temperature limits (Lorentzen
1981).
In order to calculate the efficiency of an ideal Stirling engine, the author will assume there is perfect regeneration with no regenerator dead volume. Dead volume is the total void volume in the engine and is generally referred to as the volume of working fluid contained in the total dead space in the engine (Kongtragool, Wongwises 2006).
The following (Table 1) shows energy calculations without dead volume and with perfect regeneration during the phases of the PV diagram (Fig. 8.).
In order to calculate the efficiency of an ideal Stirling engine, the author will assume there is perfect regeneration with no regenerator dead volume. Dead volume is the total void volume in the engine and is generally referred to as the volume of working fluid contained in the total dead space in the engine (Kongtragool, Wongwises 2006).
The following (Table 1) shows energy calculations without dead volume and with perfect regeneration during the phases of the PV diagram (Fig. 8.).
 |
| Table 1 Energy quantities without dead volume |
During the isochore
processes, pressure is given by:
With the pressure
obtained we can calculate the work done during both isothermal transformations
which is:
This can be
displayed to show the work for cold and hot space (Table 2). The work for a
transition is W = Wh + Wk.
 |
| Table 2 Work for cold and hot space |
Thus, the internal
efficiency of the ideal Stirling cycle will be:
Improving Efficiency
|
|
The conventional Stirling engine has the displacer and power piston
mechanically linked by a crank shaft and phased 90 degrees from each other.
However, the Martini concept assumes control of the displacer which is
independently oscillated in a reciprocating motion. The motion is controlled by
any suitable means such as an electrical motor. With the regenerator being able
to be controlled independently, this also allows for instantaneous control of
the power output of the engine by varying either amplitude or the phase angle
of the regenerator motion (Martini 1970). This concept of the engine is called the Martini Type Stirling
Engine.
The free piston Stirling engine is another configuration which aims to
improve the efficiency by having no fluid leakage. It was invented by William
Beale in 1964 (Walker, Senft 1985) (Beale 1969). The engine consists of a few numbers of components such as a piston,
displacer, springs and casing. Variations of this engine for creating
electrical power also includes a linear alternator. This model (Fig. 10.) is a
beta-type configuration and includes two linear alternators for generating
electricity (Mou, Li et al. 2016).








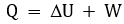






Comments
Post a Comment